Portfolio Theory
Portfolio is collection of different investments that make up an investor’s total holding. A portfolio might be:
- Investment in shares and stocks
- Investment in capital projects
Portfolio theory is concerned with establishing guidelines for building portfolios of stock and shares or portfolio of projects. Portfolio theory also assumes that investors are risk averse and will demand for higher returns for a given level of risk and the lowest risk for a given return. It also assumes that investors would always spread their risk; that is investors will spread their investments over several types of securities so that losses in some investments may be cancelled by gain from other investments. An investor who puts his entire fund in a single type of security risks everything on the fortune of the security. This means that if the security performs badly, the investor would incur huge losses.
The risk in an investment or in portfolio of an investment is the risk that the return may not be the expected return, and the actual return may be lower than the expected, or in some cases higher. A prudent investor would avoid too much risk and will hope that the actual return from his portfolio equals the expected return.
The risk is made up of two parts:
1) Alpha risk: This is also called unsystematic, specific, non-market, unique or diversifiable risk. The risk only affects a particular security.
Forms of unsystematic risk
- Business risk
- Finance risk
- Management risk (i.e. inefficient management or loss of key personnel)
2) Beta risk: This is a market imposed risk which is also referred to as systematic risk or non-specific risk.
Forms of beta risk
- Market risk
- Interest rate risk
- Purchasing power risk
- Political risk e.g war
Diversification as a means of reducing risk
The risk of a security and the risk of portfolio can be measured as the standard deviation of expected return and the risk of a portfolio depends not only on the risk of the securities making up the portfolio but also on the relationship among those securities which can be of three type:
- Positive correlation: If one investment performs well (or badly). It is likely that the other investment will perform likewise e.g. If you buy shares in a company making umbrella and in another company which sells raincoat, you will expect both companies to perform badly in dry weather.
- Negative correlation: If one investment performs well, the other will perform badly. E.g if you have shares in companies making raincoat and in another which sells ice cream. The weather would affect both companies differently.
- No correlation: The performance of one investment will be independent of how the other performs. E.g if you have shares in a mining company and in a hotel, it is likely that there would be no link between the profit and return of each company. If investments reflect high negative correlation, combination of such projects in a portfolio will reduce the overall risk. Risk will also be reduced by combining investments which have no significant correlation. The objective of diversification is to choose combination of securities with different levels of risk and return so that an acceptable return is achieved at minimum risk.
Diversification of risk
- Classify the portfolio into first class fixed income securities and equities. This guarantees the regular income from the first group and capital appreciation from the other group.
- Classify the portfolio into long and short term investment to take care of liquidity.
- Spread the fund among well rated industry but avoid concentration in companies that depend on one another or companies with identical problems
- Aim at geographical spread.
In general, negatively correlated investments should be held in order to reduce the overall risk of the portfolio because with negatively correlated investment, it is possible to eliminate the risk of portfolio.
Assumptions of portfolio theory
- Investors are rational and risk averse: The assumption that investors do not like risk is one of the foundations of portfolio theory. Without it, the entire idea of diversification becomes meaningless.
- Investors will always maximize utility which is a function of risk and expected return.
- Risk is measured by standard deviation of returns
- There are no transaction costs
- Market for security is efficient
- No taxation
- All investors are efficiently diversified
Limitations of portfolio theory
- Some projects cannot easily be divided into fractions as may be recommended by portfolio theory.
- Portfolio theory assumes that there are constant returns to scale, in order words, the percentage is deemed to be constant irrespective of the amount invested in the project.
- Portfolio theory ignores the attitude of the shareholder to risk
- Portfolio theory depends on the correct assessment of the relevant probability distribution. If the probabilities are subjective, then the conclusion would be unreliable.
- Portfolio theory is based on the concept of risk reduction through diversification. Unfortunately, investment decisions are taken by managers who cannot diversify their employment. In taking investment decisions therefore, they are concerned about total risk rather than systematic risk. Well diversified investors are only concerned about systematic risk. This brings conflict of interest between managers and shareholders.
- Portfolio theory relies heavily on mathematical manipulation that may be beyond the comprehension of many non-financial managers. In practice however, and with the spread for computing capability, the point may no longer be too relevant
Portfolio Theory
Portfolio is a collection of various investments e.g. shares, debentures or investment in factory machineries etc. Portfolio theory on the other hand provides guidelines on how to build portfolios. Portfolio theory indicates that investing has two components. I.e returns and risk. The objective of portfolio management is to maximize returns and minimize risks.
Risk can be minimized if there is effective diversification. Diversification is effective when correlation between investments is negative. Correlation can be positive, negative or neutral.
Positive correlation
Correlation is positive if the return to two investments more together i.e. increasing together or reducing together.
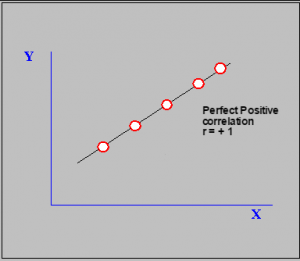
perfect positive correlation
Illustrated above is an example of perfect positive correlation
Negative correlation
The correlation between two investments is said to be negative if their returns move in opposite direction i.e when the return to one security Y for example, is increasing and that of X is reducing. Illustrated below is an example of perfect negative correlation:
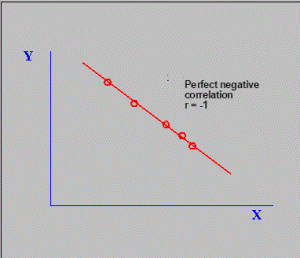
Perfect negative correlation
Neutral correlation
There is neutral correlation when the returns to two investments are unrelated. Given below is an example of zero correlation.
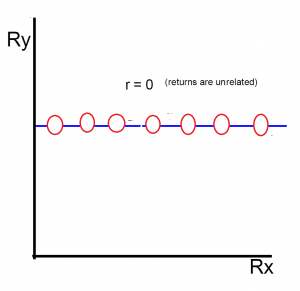
neutral correlation
As noted above, the key objective of portfolio management is maximization of returns and minimization of risk. For the purpose of portfolio theory, the risk of individual investment is irrelevant. What is relevant is the correlation between investments.
If two securities are individually risky but are inversely correlated, and a portfolio is built up, made up of security A and security B, the risk of portfolio will be considerably low, not minding the high level of risk of the individual securities. On the other hand, if two securities have low individual risks but are positively correlated, a portfolio made up of the two securities is expected to have high levels of risk, not minding the low level of risk attached to the individual securities.
The key lesson to the portfolio manager is that investment should not be evaluated in isolation but rather, we should consider their portfolio effect. The portfolio risk would be lowest if the correlation coefficient is perfect negative (-1). It would be the highest if the correlation is perfect positive (+1).
Unless otherwise stated, when we talk of risk, we are referring to standard deviation or variance. The concept of risk is defined as variability in return, hence you use standard deviation as a measure of variability in risk and return.
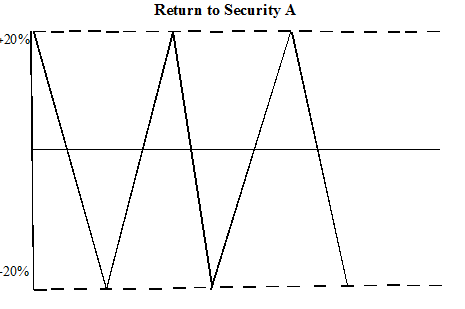
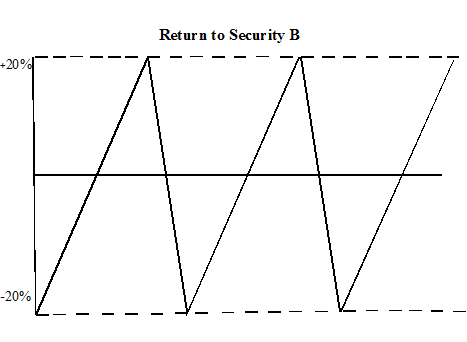
These two investments respond to the same investment differently. A could be investment in umbrella, while B could be investment in ice cream. If you build a portfolio around A and B, you can eliminate the variability when you place your money in investments that are inversely correlated.
Questions and answers on portfolio return:
What are the two required conditions for the total elimination of risk in a portfolio or investments?
For total elimination of portfolio risk (i.e standard deviation = D) the following conditions must be met:
- The correlation between the investments must be perfect negative, i.e r = -1
- The portfolio must be properly weighted (i.e the weight attached to the individual component of investment in the portfolio must be correct (right). i.e the amount to be inverted must be determined.
What are the three methods that treat risk as a function of time in investment analysis or appraisal?
Possible solution
The three methods are:
- Payback period: As it relates to risk, we say the lower the payback period, the lower the risk. The higher the payback period, the higher the risk.
- Risk Premium (e.g CAPM) : Because of the discounting effect, the higher the return, the lower the NPV you would generate.
- Finite Horison Method: In this, management sets limit of time e.g 5 years, and years after the limit would be ignored.
Expected return of portfolio
Generally, the expected return of a portfolio is given by the weighted average of the expected returns of all the securities in the portfolio. Mathematically, this can e expressed as:
RP = W1R1 + W2R2 + ………………+ WnRn
Where
RP = Expected return of portfolio
Rn = Expected return on asset n
Wn = Proportion of total funds invested in asset n or the weight of asset n
Note: W1 + W2 +…….Wn = 1 (they must add up to 1)
Recommended Readings
John L Maginn., Donald L Tuttle., Dennis W McLeavey., Jerald E. Pinto., Managing Investment Portfolios : A dynamic Process.
Frank Reily., Keith Brown., Investment Analysis & Portfolio Management
Jae sim., Joel siegel., Schaum’s outline of financial management






Leave a Reply